In the typical mathematics classroom, especially in the middle years of schooling, we tend to use one model to connect maths with the real world; we start by teaching the maths content and skills, we then get students to practice and do some maths, and then we next might apply some of those skills into a real world context by using learning activities such as word problems.
However, when you look at other models, such as those used in international assessment frameworks like PISA, you will find that a different process is modelled.
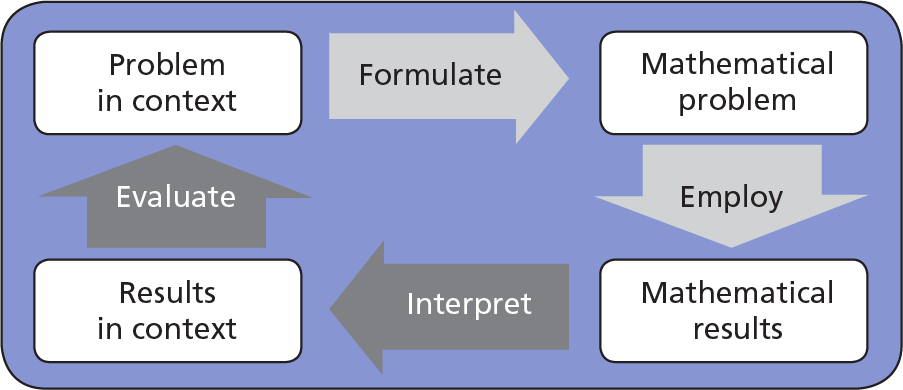
Below is the diagrammatic conception of mathematical literacy developed for PISA 2012 (OECD 2013) which is based around the need to assess students’ capacity to transfer and apply their maths knowledge and skills to problems that originate outside school-based learning contexts.
Source: OECD (2013). PISA 2012 Assessment and Analytical Framework: Mathematics, Reading, Science, Problem Solving and Financial Literacy. OECD Publishing.
The processes outlined in the model are key components of solving a real world problem, where the starting point is the problem in its context, not the maths.
- Formulating situations mathematically involves identifying how to apply and use mathematics to the problem being posed in the real world—it includes being able to take a situation and transform it into a form amenable to mathematical treatment;
- Employing mathematical concepts, facts, procedures, and reasoning involves using mathematical concepts, procedures, facts and tools to derive a mathematical solution;
- Interpreting and evaluating the mathematical outcomes involves reflecting upon mathematical solutions or results and interpreting or evaluating them back in the context of the initial problem.
This PISA process contrasts with the typical model highlighted above of: teach some maths; practice some maths; apply some maths.
The process in the real world requires a set of different skills undertaken in the reverse order – starting with the initial ability to identify the maths in the context and formulate it as a mathematical problem. Then, the second step is to do the maths, and employ skills and knowledge. Students then need to interpret and evaluate the outcomes of the maths and reflect on how the maths result(s) applies and fits in with the real world.
The first task in this PISA cycle is not something we normally address in our maths classes, yet it is possibly the most complex and difficult of all the processes.
Most of the emphasis in a typical maths classroom is on the first two processes: teach some maths; practice some maths. If we have time we may then apply that maths often through a word problem—but the maths skills have already been identified and formulated for the student (and as I said in Connecting Maths to the Real World, word problems are often not realistic or connected to real-life issues).
So, what can we do?
- Use a problem solving, investigative, open-ended approach—use real texts and real situations—make connections between maths and the real world;
- Start from the real world—teach students how to identify and extract the maths from the messy, real-life situations that they are likely to face (what I often call excavating the maths);
- Part of this is to make the maths explicit and then, when the need arises, or gaps in knowledge appear, teach the maths that is required.
For the engaged and the disengaged student, and the competent and less competent student, the context can provide the challenge, the motivation and the purpose for understanding and using mathematics. However, in order for this to work in the classroom, we need to explicitly integrate the above PISA cycle of skills into teaching and learning.
In the next article I will discuss further how such an approach might work.
References
OECD (2013a). Mathematics Framework. In OECD (2013). PISA 2012 Assessment and Analytical Framework: Mathematics, Reading, Science, Problem Solving and Financial Literacy. OECD Publishing. Retrieved from http://www.oecd.org/pisa/pisaproducts/PISA%202012%20framework%20e-book_final.pdf
As a maths teacher, how are you connecting maths and the real world in your classroom?
Do you use activities that reflect the real-life situations that your students are likely to face beyond the school gates?
What processes do you use for the formulation aspect of solving a problem?



