Teaching in context – finding the starting point looked at how you might decide on a starting point when teaching context-based maths.
The next stage in the process on how to plan your teaching this way is to investigate and document in more detail what the possible areas and topics are that could arise out of the chosen context or issue, and to decide on the actual question(s) or tasks to be undertaken.
Brainstorming
One way to undertake this is to brainstorm or develop a mind map of the topic. Don't worry at this stage about the mathematics content—finding what mathematics lies behind the issue comes later.
This usually ends up showing a wide range of related areas that could be developed further from the central theme—the challenge often is to narrow them down to one or two main starting points or questions.
You can even undertake such a brainstorm by using something concrete. This might be an actual item such as a newspaper article, a physical container (for example a high energy drink can or a packet of food), a video of an event, activity or process, a tourist map, a sports item or report, a cookbook, a pattern or plan (such as for a dress, furniture, toy or house) and more.
An example - cars
An illustration of this process is the mind map below. The topic chosen was cars - relevant to the cohort of, mainly, 16- to 17-year-old boys.
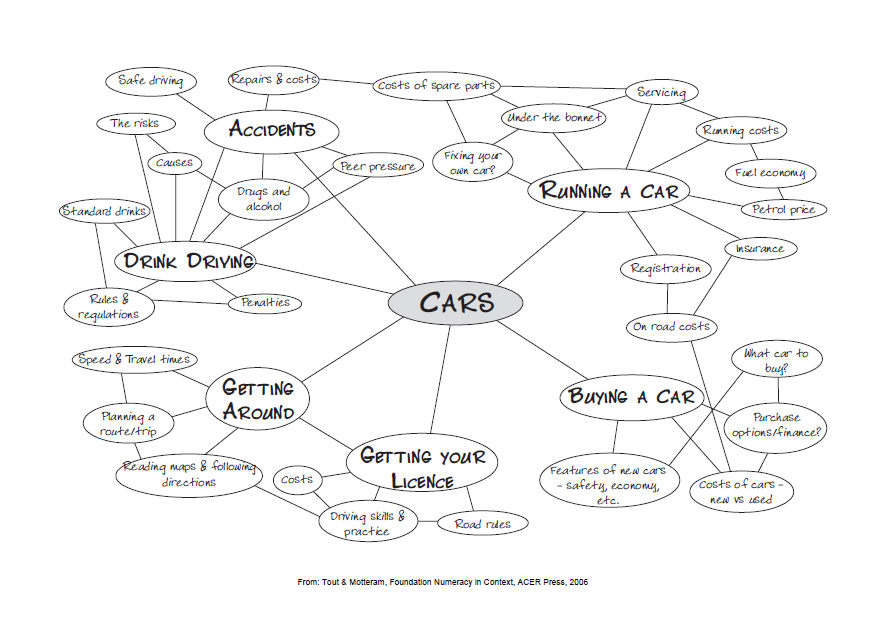
Image: Tout, D., Motteram, G. (2006). Foundation numeracy in context. Melbourne: Australian Council for Educational Research (ACER). Camberwell, Vic.
What you can see is that a large number of sub-themes arise when you think about all the different aspects of cars - buying a car, running a car, accidents, drink driving and getting around. A different teacher or group of teachers may well have come up with a completely different set of related ideas and categories and aspects of the topic.
What you often find when you do this, is that you end up with a very wide ranging spread of topics, themes, and areas, all of which are ripe for further investigation.
The next steps – identify a starting question or task
From the brainstorm diagram or list, there is the need to focus in on one or two related areas that might be of most interest to students and also enable a good range of mathematics to be investigated.
This stage involves deciding on the actual starting point and initial question(s) that will initiate the student investigation or task. This is often required because the brainstorm stage leads to too many options and pathways and because there needs to be a stronger focus on what is achievable for both the teacher and the learners.
One important ingredient is that the final investigation or task should enable students to follow their own particular approaches to the learning. It should allow them to use their own learning styles and problem solving techniques, and to build on their own interests and skills and their existing connections with the topic.
A good way of achieving this is to start with an open-ended question—one that arises out of the brainstorm, but that enables students to go off in their own direction and use their own skills and knowledge.
On the other hand, it cannot be too open-ended, as this could lead to students doing completely different tasks and investigations, and requiring quite different mathematical skills. So there is a need as the teacher to structure the task so that most student investigations will require the use of similar mathematics skills and understandings.
In relation to the sample brainstorm provided above about cars, some possible open-ended questions to pose to students could be:
- If you had $10,000 to spend on a car, what car would you buy? Why? Where from? Describe the car you would buy and why you wanted it.
- How could you pay for a car worth $12,000? Compare at least three different ways.
- Once you have bought a car, what are the different running costs for cars? How do their costs compare?
- Are young people more likely to die in car accidents than older drivers?
- What does Blood Alcohol Content (BAC) mean and how do different drinks affect Blood Alcohol Content?
- How do Global Positioning Systems (GPS) work in cars?
In most cases, you would only choose one of these for a group of students, although you may be able to offer two related questions.
Next steps
The next stage in planning your teaching so that maths is connected to real life situations is to identify where the mathematics that is embedded within the chosen topic and the theme that lies behind the particular starting question(s). This will be addressed in the next article.
References
Tout, D., Motteram, G. (2006). Foundation numeracy in context. Melbourne: Australian Council for Educational Research (ACER). Camberwell, Vic.
What strategies do you use for planning how to use a problem solving process in your classroom?
When choosing a topic, how will you involve students in the decision making process?
Is there an opportunity to incorporate mind mapping at the start of your next topic?



