In the final instalment of our three part series on the International Mathematical Modelling Challenge (IMMC), Ross Turner outlines the mathematical modelling framework and provides some practical advice on approaching the ‘jet lag' problem set for the 2017 challenge.
Strengthening the connection between mathematical knowledge and skills, and the ways in which they can be used, is a central objective of many approaches to mathematics teaching and learning.
The IMMC provides a very direct opportunity to develop the relevant capabilities. It's a team-based competition where up to four students from the same school are given five days to work on a modelling task (located in a real-world setting), write a report and submit it for evaluation.
Australia's participation in the IMMC has been led and overseen by the Australian Council for Educational Research (ACER). An overarching objective of the challenge is to encourage and facilitate change in some of the classroom practices of mathematics teachers and learners.
What is the mathematical modelling framework?
The aim of IMMC is to produce students who can identify and effectively solve real-world problems. The following seven-step framework – which can be found on the Australian Challenge website – helps students take a systematic approach to devising solutions.
- Describe the real-world problem. Identify and understand the practical aspects of the situation.
- Specify the mathematical problem. Frame the real-world scenario as an appropriate, related mathematical question(s).
- Formulate the mathematical model. Make simplifying assumptions, choose variables, estimate magnitudes of inputs, justify decisions made.
- Solve the mathematics.
- Interpret the solution. Consider mathematical results in terms of their real-world meanings.
- Evaluate the model. Make a judgment as to the adequacy of the solution to the original question(s). Modify the model as necessary and repeat the cycle until an adequate solution has been found.
- Report the solution. Communicate clearly and fully your suggestions to address the real-world problem.
Students may need to repeat four of the steps (formulate, solve, interpret and evaluate) several times before they reach a successful solution.
The IMMC ‘jet lag' problem
The ‘jet lag' problem set for the 2017 challenge began: “Organizing international meetings is not easy in many ways, including the problem that some of the participants may experience the effects of jet lag after recent travel from their home country to the meeting location which may be in a different time-zone, or in a different climate and time of year, and so on. All these things may dramatically affect the productivity of the meeting.”
Student teams were tasked with creating an algorithm to produce a list of recommended places to hold a meeting, with the aim being to maximise overall productivity. They were asked to test their algorithm on two datasets:
Scenario 1 “Small Meeting”. Time: mid-June. Six individual participants from: Monterey CA, USA; Zutphen, Netherlands; Melbourne, Australia; Shanghai, China; Hong Kong (SAR), China; Moscow, Russia
Scenario 2 “Big meeting”. Time: January. Eleven individual participants from: Boston MA, USA (2 people); Singapore; Beijing, China; Hong Kong (SAR), China (2 people); Moscow, Russia; Utrecht, Netherlands; Warsaw, Poland; Copenhagen, Denmark; Melbourne, Australia.
The modelling process
An essential starting point is to clarify exactly what the IMMC problem required. The problem statement asks teams to develop an algorithm and test it on at least two given scenarios. It is worthwhile emphasising that the question does not ask where those two meetings should be held, but asks for a systematic process (an algorithm) that could be followed to determine a location for a meeting of participants from different home locations that maximises productivity of the participants, especially in relation to the effects of jet lag.
A further essential step in an effective modelling activity is to transform the statement of what is required in relation to the problem statement and its real-world setting, into a mathematical objective. As well as developing a clear understanding of what would constitute an answer to the question in the context from which it came, the goals of the exercise must also be expressed in clear mathematical terms. For example, the mathematical objective could be to minimise total distance travelled by the meeting participants, or time spent travelling, and so on.
The end-point of the modelling process is to communicate the results of the modelling work in a form that can be understood and used by its intended audience. The form of the product required for the IMMC comprises three parts: a one-page summary sheet, a report of the solution, and appendices including references used. However, the exact way a report is constructed should be determined in light of its purpose and audience. A modelling report is not the same thing as a school mathematics assignment. It might often take the form of a recommendation or set of recommendations to a committee, together with an explanation and justification of the recommendations.
In between the beginning process of defining the goals of the task and defining that in mathematical terms, and the end process of writing a report, the processes of model formulation, mathematical processing, and model evaluation take place. Those processes would often occur multiple times, since a first attempt at solving the problem might expose further issues that should be taken more effectively into account to provide the best possible solution to the problem at hand. A better mathematical formulation might be needed, an adjusted model might then be required, a different kind of mathematical processing could assist, and an updated interpretation of the results and evaluation of the outcomes would then be needed.
Approaches taken by Australian teams
Identifying relevant variables. Some factors that were said to be important included: time zone changes; climate; weather; characteristics of the destination city; hours of sunlight; optimal working conditions; and activities outside of the meeting. A key issue then was the extent to which factors said to be important were treated effectively in the solution rocess.
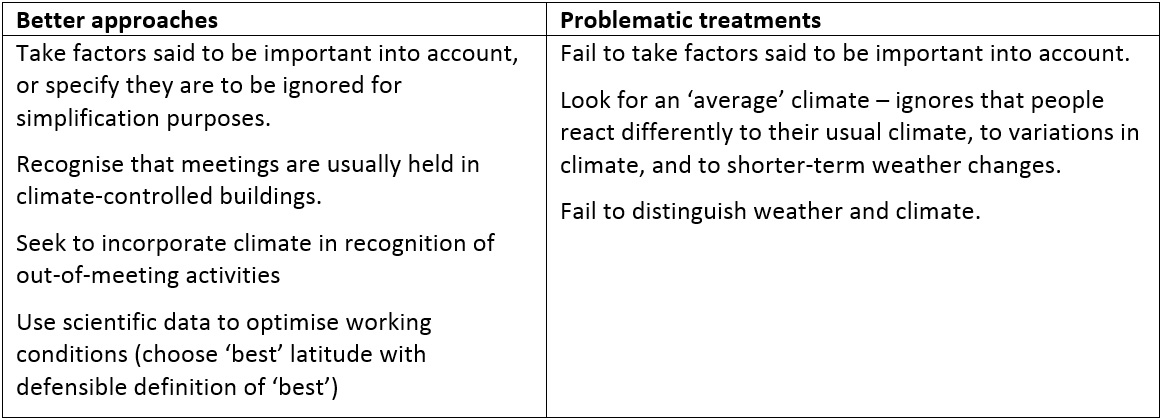
Identifying assumptions, and other factors. A key feature of mathematical modelling is the need to identify assumptions that are made, and to explain why they are made; also to consider how the assumptions made influence the solution found, and how changing assumptions might affect the solution. Other factors that could be considered include: the difference in jet lag effect between travel towards the east and west; the added impact of travel fatigue; and the possible addition of consideration of cost-related factors.

How ‘distance travelled' was treated. Some of the considerations that were important here were: considering ‘as the crow flies' versus plausible flight routes; whether minimising distance travelled would alone solve the problem; consideration of journey time (for example, whether direct or multiple flights might be needed); accuracy of complex distance calculations.

How time zones were treated. Relevant factors here were: it was essential to use some absolute reference system – most teams used Universal Coordinated Time (UTC) as a reference; the degree of overlap of ‘alert' periods for participants; accuracy in calculations of time zones for different locations and different times of the year; and the treatment of ‘recovery time'.
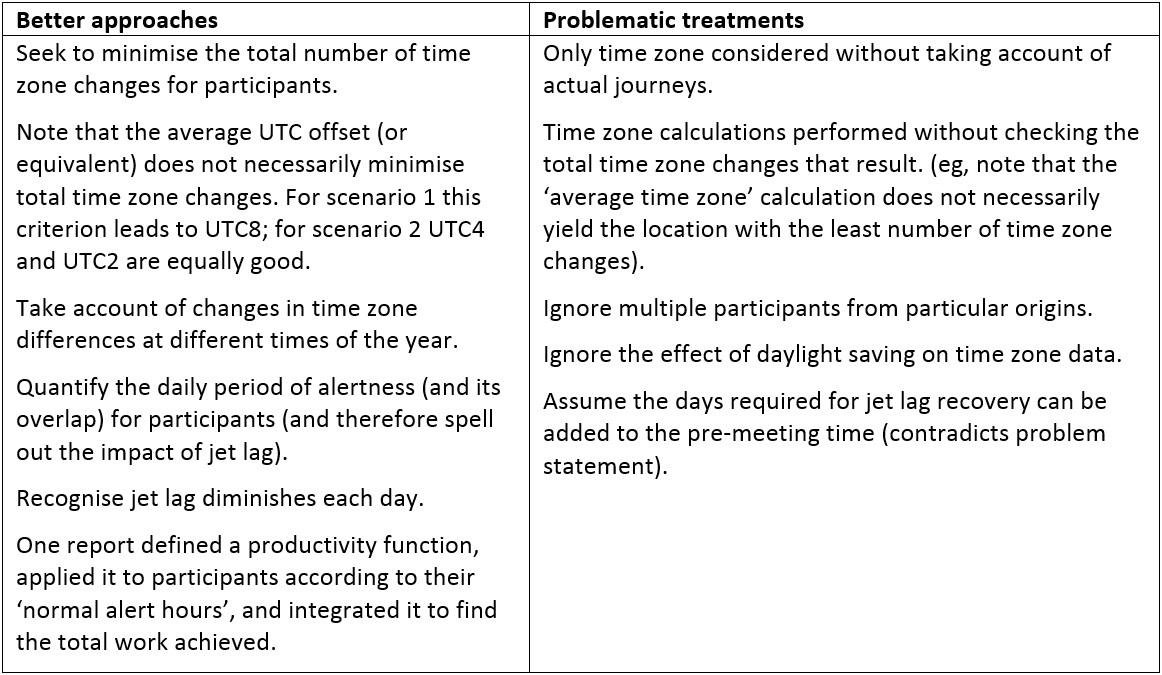
Sensitivity analysis, solution evaluation. Finally, no modelling process is complete without an evaluation of the solution proposed. Does the proposed solution answer the question? How would a change in the assumptions or starting conditions affect the solution found? What additional factors could be taken into account to make the solution work in a wider variety of circumstances? Very few of the IMMC 2017 reports considered the extent to which their solution was ‘best' and what other possible solutions might have been equally or almost as good. Very few teams showed that their solution would apply to completely different scenarios from the two cases given in the problem statement.

The IMMC Australian website includes free resources for teachers. Educators can download example problems for general use in maths teaching.
Think about an upcoming topic you’re teaching. How can you incorporate classroom activities that reflect real-life situations?



